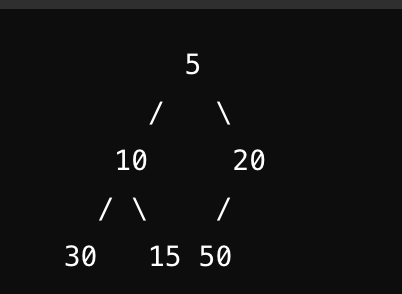
개요
- Tree의 개념에 대해 파악해보고, Heap과 BST에 대해 알아봅시다
Heap (완전 이진 트리)
- 완전 이진 트리 형태이다
- 값의 규칙
- 최대 힙: 부모노드 >= 자식노드
- 최소 힙: 부모노드 <= 자식노드
- 이런식으로 두가지 경우의 Heap Tree가 존재한다는 의미이다.
- 최대 힙: 부모노드 >= 자식노드
- 설계이유
- 최대값,최소값을 기준으로 처리해야할때 용이하다
- 예시코드
import java.util.PriorityQueue;
public class TaskScheduler {
static class Task {
int priority;
String name;
Task(int priority, String name) {
this.priority = priority;
this.name = name;
}
@Override
public String toString() {
return "Task{name='" + name + "', priority=" + priority + "}";
}
}
public static void main(String[] args) {
// 우선순위가 높은 작업부터 처리하는 최대 힙
PriorityQueue<Task> maxHeap = new PriorityQueue<>((a, b) -> b.priority - a.priority);
// 작업 추가
maxHeap.add(new Task(3, "Task A"));
maxHeap.add(new Task(5, "Task B"));
maxHeap.add(new Task(1, "Task C"));
maxHeap.add(new Task(4, "Task D"));
// 작업 처리
System.out.println("Processing tasks by priority:");
while (!maxHeap.isEmpty()) {
System.out.println(maxHeap.poll());
}
}
}
- poll()사용시 루트노드부터 내려오기 때문에 5,4,3,1 순으로 나온다
- 현재 Tree Heap 설계시, new PriorityQueue<>((a, b) -> b.priority - a.priority);
- 이런식으로 역방향을 걸어주었기 때문에 최대 힙 상태가 된다
BST (일반 이진 트리)
- 일반 이진 트리이다
- 값의 규칙
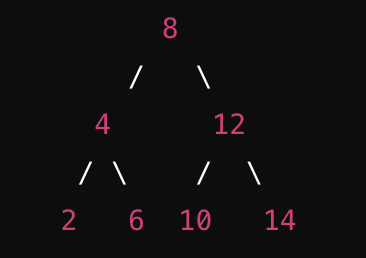
- 왼쪽 노드 < 부모 노드 < 오른쪽 노드
- 이런 느낌이다
- 설계이유
- 빠른 검색, 정렬된 데이터 저장
- 예시를 들어보자 (균형이 잡힌 트리 기준)
- 10개의 데이터(1,2,3 ... 10)가 ArrayList, BST로 구성되어있을때의 예시다
- 인덱스가 5인 데이터를 찾는다고 가정해보자
- ArrayList:
- 인덱스기반으로 찾을때는 O(1)의 시간 소요
- BST:
- 인덱스기반으로 찾는다는건 말이안된다
- ArrayList:
- 숫자 5를 찾는 다고 가정해보자
- ArrayList:
- 특정 숫자의 데이터를 찾아야하기 때문에 O(n)의 시간이 소요
- BST:
- 빠른검색답게, O(log n)의 시간이 소요된다
- ArrayList:
- 왜 빠른 검색이 가능할까?
- BST는 부모 노드는, 왼쪽 노드보다 작고, 오른쪽 노드보다 크다는 특징이 있습니다
- 각 노드의 값을 비교하며, 불필요한 서브트리에 방문하지않는 가지치기 과정덕분에, 효율적인 검색이 가능
- Ex)

- 다음과 같은 일반 이진트리에서 12를 찾는 동작과정을 기재해보도록 하자
- 10방문 (찾으려는 데이터가 현재 노드보다 크면 오른쪽, 아니면 왼쪽) - 오른쪽 선택
- 15방문 (찾으려는 데이터가 현재 노드보다 크면 오른쪽, 아니면 왼쪽) - 왼쪽 선택
- 12방문 (찾음)
- 위 예시는 빠른검색을 사용할때의 동작과정을 알아보았다
- 또 다른 동작과정인 중앙순회 방식이다
- 이 방식은 일반 이진 트리구조의 데이터를 정렬된 상태로 나열하기위해 사용되는 방식이며
- 왼쪽노드 -> 부모노드 -> 오른쪽노드 이런순서다
- Ex)
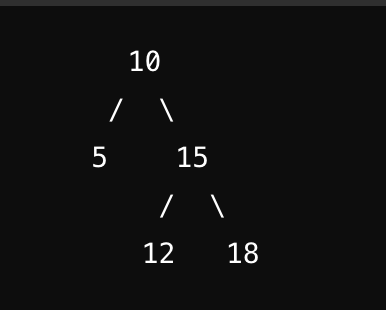
- 5 -> 10 -> 12 -> 15 -> 18
- 이런 느낌이다
나는 오늘 무엇을 알았는가?
- Tree는 비선형자료구조이다
- 계층적 자료구조임
- Heap(완전 탐색 트리)은 최대,최소의 데이터를 찾을때 유용하다
- BTS(이진 탐색 트리)는 빠른 검색을 할때 유용하다
TMI 1

- 어째서 이 자료구조에서 왼쪽의 서브트리는 3 5 7 형태를 하고있을까?
- 왜 4 5 7 은 안되는걸까?
- 정답은 1~20 까지의 배열을 예시로 하였기 때문에 3이 들어간것이다
- 만약 1,2,4, ... , 21 까지의 배열이였다면 4가 들어갔을것이다
- 트리는 주어진 데이터 집합으로만 구성된다!
TMI 2
- 완전 이진 트리 (Heap), 이진 트리(BT)의 차이가 무엇일까 ?
Heap
- 왼쪽에서 오른쪽으로 채워지는 트리
- 트리의 마지막 레벨을 제외한 모든 레벨이 꽉차있어야함
- 마지막 레벨에서는 노드가 왼쪽에서 오른쪽 순서로만 채워져야함
- 1~4라는 데이터로 트리를 구성해보자
1 / \ 2 3 / 4 - 위 특성떄문에 이런식의 트리만 구성되지만
- BT의 경우는 다르다
BT
- 이진트리는 자식노드가 2개를 초과하지 않으면 자유롭게 구성가능하다
- 즉 아래와같은 형식들이 가능하다는 뜻이다
1 / \ 2 3 \ 4
1
/
2
/
3 /
4
- 이런 차이가 있는것이다
'Cs' 카테고리의 다른 글
| CS 기초 공부 - IP 주소 (0) | 2025.01.23 |
|---|---|
| 자료구조 (1) | 2025.01.23 |
| TCP/IP 4계층 모델이란 ? (1) | 2025.01.22 |
| 사이드 이펙트란? (0) | 2025.01.21 |
| 비트마스크란 ? (1) | 2025.01.19 |