개요
- Tree에 대한 이론을 배웠고, 기본적인 형태를 직접 구성해보며 알아보자
각각의 트리에 대해 실습해보자
- 일반 트리 (N-ary Tree)
- 이진 트리 (Binary Tree)
- 이진 탐색 트리 (BST)
- 균형 트리 (AVL, Red-Black)
- 힙 (Heap)
- 트라이 (Trie)
이진 트리 (Binary Tree)
- 각 노드가 최대 2개의 자식 노드를 가질 수 있는 트리구조
package tree.binaryTree;
class Node {
int v;
Node left;
Node right;
public Node(int v) {
this.v = v;
left = null;
right = null;
}
public void print(String prefix) {
System.out.println(prefix + v);
if (left != null) {
left.print(prefix + "-");
}
if (right != null) {
right.print(prefix + "-");
}
}
}
public class Main {
public static void main(String[] args) {
Node root = new Node(1);
root.left = new Node(2);
Node left = root.left;
left.left = new Node(4);
left.right = new Node(5);
root.right = new Node(3);
Node right = root.right;
right.left = new Node(6);
right.right = new Node(7);
root.print("");
}
}
print의 결과를 예상해보자
- 1
- -2
- --4
- --5
- -3
- --6
- --7
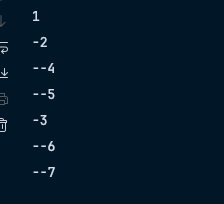
잘나오는 모습이다
문제
- 📘 문제 설명
- 숫자로 구성된 배열이 주어진다. 이 숫자들을 이진 탐색 트리(BST)로 삽입한 뒤,
트리의 다음 기능들을 구현하라
- 숫자로 구성된 배열이 주어진다. 이 숫자들을 이진 탐색 트리(BST)로 삽입한 뒤,
- ✨ 조건
- 이진 탐색 트리(BST)는 왼쪽 자식은 자기보다 작고, 오른쪽 자식은 자기보다 큰 값을 가진다.
- 중복된 값은 무시한다.
- 🔨 구현해야 할 메서드
- 클래스 BinarySearchTree와 Node를 만들어서 다음 메서드를 구현하라.
package tree.binaryTree;
class Node {
int value;
Node left;
Node right;
// 생성자
}
class BinarySearchTree {
Node root;
public void insert(int value) {
// DFS 방식으로 트리에 값 삽입
}
public boolean search(int value) {
// DFS 방식으로 값 존재 여부 탐색
return false;
}
public void inorder(Node node) {
// DFS 방식의 중위 순회 출력
// (왼 → 중 → 오)
}
public int countNodes(Node node) {
// DFS 방식으로 전체 노드 수 계산
return 0;
}
public static void main(String[] args) {
int[] arr = {5, 3, 7, 2, 4, 6, 8};
}
}
Insert
public void insert(int value) {
root = insert1(root,value);
}
public Node insert1(Node cur, int value){
if (cur == null) {
return new Node(value);
}
if (cur.value > value) {
cur.left = insert1(cur.left,value);
}
else if (cur.value < value) {
cur.right = insert1(cur.right,value);
}
return cur;
}- 실행 흐름을 예상해보자
- value로 5가 들어간다
- 현재 tree의 root는 null이기 때문에, value값이 5가 들어가있는 Node가 채워진다
- 그 다음 value 3이 들어온다
- 현재 tree의 root의 value는 5이기 때문에 5>3으로, 첫번째 분기점에 걸린다 (현재 노드보다 작다면 왼쪽, 크다면 오른쪽이기때문)
- 인자로 cur.left를 넣어주고, 파라미터로받은 3을 그대로 넣어준다
- cur.left -> cur이 되면서, cur은 null이기때문에 3을 넣어준다
- 그다음 7이 들어온다
- 현재 root는 root.value = 5, root.left = 3, root.right = null 상태이다
- 5<7이므로 두번째 분기점에 걸린다
- 파라미터로 cur.right를 넣어주지만, 이것은 null값이기떄문에
- 재귀로 호출된 cur == null분기점에 걸리며
- 현재 root.value = 5, root.left = 3, root.right = 7인상태가된다
- 다음 2가 들어온다
- 5>2이기 때문에 첫번째 분기점에 걸린다
- root.left는 현재 3이다
- 따라서 재귀로 호출된 insert1에서는 다시
- 3>2 상태가 되고 첫번째 분기에 똑같이 걸리면서
- 3의 left를 파라미터로 넣는다
- 따라서 현재 root.value = 5, root.left = 3, root.right = 7 root.left.left = 2상태이다
Chatgpt 요약
초기 상태
root = null삽입 순서
5, 3, 7, 2, 4, 6, 8
1. 5 삽입
root == null→ 새로운 Node(5) 생성 →root = Node(5)
2. 3 삽입
root.value(5) > 3→ 왼쪽으로 이동root.left == null→ Node(3) 생성 →root.left = Node(3)
3. 7 삽입
root.value(5) < 7→ 오른쪽으로 이동root.right == null→ Node(7) 생성 →root.right = Node(7)
4. 2 삽입
5 > 2→ 왼쪽 (3)3 > 2→ 왼쪽3.left == null→ Node(2) 생성 →root.left.left = Node(2)
5. 4 삽입
5 > 4→ 왼쪽 (3)3 < 4→ 오른쪽3.right == null→ Node(4) 생성 →root.left.right = Node(4)
6. 6 삽입
5 < 6→ 오른쪽 (7)7 > 6→ 왼쪽7.left == null→ Node(6) 생성 →root.right.left = Node(6)
7. 8 삽입
5 < 8→ 오른쪽 (7)7 < 8→ 오른쪽7.right == null→ Node(8) 생성 →root.right.right = Node(8)
search
public boolean search(int value) {
return search1(root, value) != null;
}
public Node search1(Node node, int compareValue) {
if (node == null) return null;
if (node.value == compareValue) return node;
if (search1(node.left, compareValue) != null) return search1(node.left, compareValue);
if (search1(node.right, compareValue) != null) return search1(node.right, compareValue);
return null;
}- 실행 흐름을 알아보자
- 1번째 스택메모리에서 현재 노드의 5를 비교하였지만 다름, 따라서 left search구문을 타고들어감
- 2번쨰 스택메모리에서도 현재 노드의 3을 비교하였지만 다름, 따라서 left search 구문을 타고들어감
- 3번째 스택메모리에서도 현재 노드의 2를 비교하였지만 다름, 따라서 left search 구문을 타고들어감
- 4번쨰 스택메모리에서의 node는 null이기 때문에 return
- 3번째 스택메모리로 돌아가 right search 구문을 타고들어간다
- 4번째 스택메모리서의 node도 null이기때문에 return
- 3번째 스택매모리로 복귀후, left,right search구문이 전부 수행되었음에도 null이기때문에, 마 지막 로직인 null이 반환된다
- 2번째 스택메모리로 복귀후, left search의 결과가 null이기때문에, right search구문을 타고들어간다
- 3번쨰 스택메모리에서의 node가 4로 동일한 node를 발견한후 반환한다
- 2번쨰 스택메모리로 복귀후, node가 null이 아니기 떄문에, 4 node를 반환한다
- 1번쨰 스택메모리로 복귀후, left search의 결과가 node4를 반환하였기떄문에 그대로 반환한다
Chatgpt 요약
🔄 전체 흐름 설명
- 현재 노드의 값이 찾는 값인지 확인
- 맞으면 해당
Node를 즉시 반환 - 아니라면 왼쪽 자식 노드부터 탐색 시작
- 맞으면 해당
- 왼쪽 서브트리 탐색
search1(node.left, compareValue)호출- 결과가
null이 아니면, 해당 노드를 반환
- 왼쪽에서 못 찾은 경우 오른쪽 서브트리 탐색
search1(node.right, compareValue)호출- 결과가
null이 아니면, 해당 노드를 반환
- 좌우 모두 못 찾은 경우
- 최종적으로
null반환
- 최종적으로
✅ 스택 메모리 흐름 예시 (compareValue = 4)
트리 구조:
5
/ \
3 7
/ \ / \
2 4 6 8search1(5, 4)→ 5는 아님 → 왼쪽 탐색search1(3, 4)→ 3은 아님 → 왼쪽 탐색search1(2, 4)→ 2는 아님 → 좌우 null → return nullsearch1(3, 4)오른쪽 탐색 →search1(4, 4)→ 찾음! → return Node(4)- 상위 함수들도 그대로
Node(4)리턴하면서 스택에서 차례로 복귀
inorder
public void inorder(Node node) {
if (node == null) return;
inorder(node.left);
System.out.println(node.value);
inorder(node.right);
}- 실행 흐름을 분석해보자
- 1번째 스택메모리 (5)는 null이 아니라 패스후, inorder(left)구문을 탄다
- 2번째 스택메모리 (3)은 null이 아니라 패스후, inorder(left)구문을 탄다
- 3번째 스택메모리 (2)는 null이 아니라 패스후, inorder(left)구문을 탄다
- 4번째 스택메모리 (?)는 null이므로 return
- 3번쨰 스택메모리 (2)에서 현재 노드인 2를 출력한다, inorder(right)구문을 탄다
- 4번째 스택메모리 (?)는 null이므로 return
- 3번째 스택메모리의 메서드가 모두 종료되어서 이전 스택메모리로 복귀한다
- 2번째 스택메모리 (3)에서 현재 노드인 3을 출력한다, inorder(right)구문을 탄다
- 3번째 스택메모리에서 (4)는 null이 아니라 패스후, inorder(left)구문을 탄다
- 4번쨰 스택메모리 (?)는 null이므로 return
- 3번쨰 스택메모리에서 현재 노드인 4를 출력한다, inorder(right)구문을 탄다
- 4번쨰 스택메모리 (?)는 null이므로 return
- 3번쨰 스택메모리에서의 모든 메서드가 종료되어, 이전 스택메모리로 복귀한다
- 2번째 스택메모리에서의 모든 메서드가 종료되어, 이전 스택메모리로 복귀한다
- 1번쨰 스택메모리에서 현재 노드인 5를 출력한다, inorder(right)구문을 탄다
... 반복
chatgpt 요약
- 1번째 스택:
inorder(5)→node.left호출 - 2번째 스택:
inorder(3)→node.left호출 - 3번째 스택:
inorder(2)→node.left호출 - 4번째 스택:
inorder(null)→ return - 3번째 스택:
2출력 →node.right호출 - 4번째 스택:
inorder(null)→ return - 3번째 스택 종료 → 복귀
- 2번째 스택:
3출력 →node.right호출 - 3번째 스택:
inorder(4)→node.left호출 - 4번째 스택:
inorder(null)→ return - 3번째 스택:
4출력 →node.right호출 - 4번째 스택:
inorder(null)→ return - 3번째 스택 종료 → 복귀
- 2번째 스택 종료 → 복귀
- 1번째 스택:
5출력 →node.right호출 - 2번째 스택:
inorder(7)→node.left호출 - 3번째 스택:
inorder(6)→node.left호출 - 4번째 스택:
inorder(null)→ return - 3번째 스택:
6출력 →node.right호출 - 4번째 스택:
inorder(null)→ return - 3번째 스택 종료 → 복귀
- 2번째 스택:
7출력 →node.right호출 - 3번째 스택:
inorder(8)→node.left호출 - 4번째 스택:
inorder(null)→ return - 3번째 스택:
8출력 →node.right호출 - 4번째 스택:
inorder(null)→ return - 모든 스택 종료
countNodes
public int countNodes(Node node) {
if (node == null) return 0;
int l = countNodes(node.left);
int r = countNodes(node.right);
return 1 + l + r;
}- 실행 흐름을 분석해보자 (node는 root기준)
- 1번째 스택메모리(5)에서 countNodes(left) 구문을 타고들어간다
- 2번째 스택메모리(3)에서 countNodes(left) 구문을 타고 들어간다
- 3번째 스택메모리(2)에서 countNodes(left) 구문을 타고 들어간다
- 4번째 스택메모리(?)에서 null이므로 0을 반환한다
- 3번째 스택메모리(2)에서 countNodes(left)는 0이다, countNodes(right) 구문을 타고 들어간다
- 4번쨰 스택메모리(?)에서 null이므로 0을 반환한다
- 3번째 스택메모리(2)에서 countNodes(right)는 0이다, 따라서 return 1+0+0을 하며 메서드가 종료되며 이전 스택메모리로 복귀한다
- 2번째 스택메모리(3)에서 countNodes(left)는 1을 가지고 있는 상태, countNodes(right)구문을 타고 들어간다
- 3번째 스택메모리(2)와 같은 과정을 진행하게되는데, 여기서 스택메모리의 노드는(4)기준으로 한다
- 2번쨰 스택메모리의 countNodes(left), countNodes(right)는 현재 1,1인 상태이이므로, return 1+1+1 을 반환한다, 현재 스택 메모리의 메서드가 모두 종료되었기 떄문에 이전 스택메모리로 복귀한다
- 1번째 스택메모리의 countNodes(left)는 3인 상태, 그다음인 countNodes(right)에 간후에 동일하게 진행되어 countNodes(right)도 3이되며, 최종적으로 1+3+3 을반환하게되며 7이된다
chatgpt 요약
- 1번째 스택 (5):
countNodes(5)→countNodes(3)호출 - 2번째 스택 (3):
countNodes(3)→countNodes(2)호출 - 3번째 스택 (2):
countNodes(2)→countNodes(null)→ return 0 - 3번째 스택 (2): 오른쪽도
null→ return 0 →return 1 + 0 + 0 = 1 - 2번째 스택 (3): 왼쪽 결과는 1 →
countNodes(4)호출 - 3번째 스택 (4): 왼쪽
null→ 0, 오른쪽null→ 0 →return 1 + 0 + 0 = 1 - 2번째 스택 (3): 왼쪽 1, 오른쪽 1 →
return 1 + 1 + 1 = 3 - 1번째 스택 (5): 왼쪽 결과는 3 →
countNodes(7)호출 - 2번째 스택 (7):
countNodes(6)호출 → 좌우null→ return 1 - 2번째 스택 (7):
countNodes(8)호출 → 좌우null→ return 1 - 2번째 스택 (7): 왼쪽 1, 오른쪽 1 →
return 1 + 1 + 1 = 3 - 1번째 스택 (5): 왼쪽 3, 오른쪽 3 →
return 1 + 3 + 3 = 7
마무리
- 모든 메서드를 구현해보았다
- 다음은 이진 탐색 트리 (BST)에 대해 공부해보자
'Cs' 카테고리의 다른 글
| Tree를 직접 구현해보자 - 1 (1) | 2025.03.25 |
|---|---|
| HTTPS ? (0) | 2025.01.28 |
| CS 기초 공부 - IP 주소 (0) | 2025.01.23 |
| 자료구조 (1) | 2025.01.23 |
| Tree ? (1) | 2025.01.22 |